流體力學理論與F1賽車的空氣動力學（一）

2017-03-19 by:CAE仿真在線來源:互聯網

第一

理論基礎

1.概況與發展歷程

流體力學,是研究流體(液體和氣體)的力學運動規律及其應用的學科。主要研究在各種力的作用下,流體本身的狀態,以及流體和固體壁面、流體和流體間,流體與其他運動形態之間的相互作用的力學分支。它主要研究流體本身的靜止狀態和運動狀態,以及流體和固體界壁有相對運動時的相互作用和流動的規律。按照研究對象的運動方式可將其分為流體靜力學和流體動力學,還可按流動物質的種類分為水力學,空氣動力學等等。描述流體運動的基本方程是納斯-斯托克斯方程,簡稱N-S方程。
筆者注:N-S方程基于牛頓第二定律,表示流體運動與作用于流體上力的相互關系,N-S方程是非線性微分方程,其中包含流體的運動速度、壓強、密度、粘度、溫度等變量,而這些都是空間位置和時間的函數。一般來說,對于一般的流體學問題,需要將N-S方程結合質量守恒,能量守恒、勢力學方程以及介質的材料性質,一同求解。由于其復雜性,通常只有通過給定邊界條件下,通過計算機才可求解。
空氣動力學是流體力學的一個重要分支,主要研究空氣或其它氣體的運動規律、空氣或其它氣體與飛行器或其他物體相對運動時的相互作用和伴隨產生的物理變化。
根據空氣與物體的相對速度,可將空氣動力學分為低速空氣動力學(相對速度小于100m/s,即360km/h)和高速空氣動力學,也有學說將界限劃定為400km/h。前者屬于不可壓縮流動的空氣動力學,后者屬于可壓縮流動的空氣動力學。一般來說,空氣流速小于0.3馬赫時,氣體是不可壓縮流動的,大于這個數值則被理解為可壓縮流動。F1所研究的空氣動力學屬于低速范疇。此外,還根據是否忽略氣流的粘性,將空氣動力學分為理想空氣動力學和粘性空氣動力學。
20世紀初,飛機的出現極大地促進了空氣動力學的發展。航空事業的發展,需要揭示飛行器周圍的壓力分布、飛行器受力狀況和阻力等問題,這就促進了流體力學在實驗和分析方面的發展。20世紀初,以無粘不可壓縮流體位勢流理論為基礎的機翼理論,闡明了機翼怎樣受到舉力,從而將很重的飛機托上天空,機翼理論的正確性,使人們重新認識到無粘理論,肯定了其指導工程設計的重大意義。
機翼理論和邊界層理論的建立和發展是流體力學的一次重大進展,它使無粘流體理論同粘性流體的邊界層理論很好地結合起來。隨著汽輪機的發展和飛機的飛行速度提高到每秒50米以上,又迅速擴展了對空氣密度變化的效應和理論研究,這高速飛行提供了理論指導。
從50年代起,數學的發展,電子計算機的不斷完善,以及流體力學各種計算方法的發明,使得許多原本無法用理論分析求解的復雜流體力學問題有了求得數值的可能性,并以此形成了計算流體力學,此后,模型法、CFD技術、風洞測試等新興手段的介入使得該學科取得了飛躍性的進步。

運用到F1領域的CFD技術。

法拉利位于總部馬拉內羅的風洞

F1的空氣動力學主要研究下壓力,阻力和靈敏度三個方面,其中,提高壓力是提升彎中表現的有效手段,降低阻力是獲得高尾速輸出的必要手段,靈敏性又稱敏感度,主要研究空氣動力學環境改變而導致的自身變化的強度。確切地說,就是研究由路況差異而導致的氣動翼片與底盤間距的變化對賽車性能的干預強弱。以上三大課題,決定著一輛F1賽車的整體氣動性能。

2.基本概念

(1)流體
流體,顧名思義,就是可以流動的物體,是液體和氣體的總稱,是由大量的、不斷地作熱運動而且無固定平衡位置的分子構成的,其基本特征是沒有一定的形狀和具有流動性。流體都有一定的壓縮性,液體的可壓縮性很小,而氣體的可壓縮性較大,在流體形狀發生改變時,流體各層間也存在一定的運動阻力(即粘滯性)。當流體的粘滯性和可壓縮性很小時,可近似看作是理想流體,它是人們為研究流體的運動狀態而引入的一個理想模型。
流體與固體在某些方面有著非常明顯的差別:Ⅰ在靜止的狀態下固體的作用面上能夠同時承受剪切應力和法向應力,而流體則只有在運動的狀態下才能夠同時受到這兩種力的作用(在靜止狀態下其作用面上僅能夠承受法向應力,即為靜壓強)。Ⅱ固體在力的作用下發生變形,在彈性限度內形變和作用力之間服從胡克定律,即固體的形變量和作用力的大小成正比。而流體則是角變形速度與剪切應力有關,層流和紊流狀態使它們之間的關系有所不同。在層流狀態下,二者之間服從牛頓內摩擦定律。Ⅲ當外力停止作用時,固體可以恢復為原來的形狀,而流體由于其形變所需的剪切應力非常小,所以很容易使自身的形狀適應容器的形狀,并可在一定的條件下維持下來。

(2)流體的粘滯性
前文中提到過,當流體的粘滯性與可壓縮性很小時,可以稱之為理想流體。然而,對于一般的流體來說,粘滯性是一種重要而且普遍的性質。
流體力學中這樣給粘滯性定義:流體在受到外部剪切力作用時發生變形(流動),內部相應要產生對變形的抵抗,并以內摩擦的形式表現出來。所有流體在相對運動時都要產生內摩擦力,這是流體的一種固有的物理屬性。
牛頓內摩擦定律或牛頓剪切定律對流體的粘性作了理論的描述,即流體層之間單位面積的內摩擦力或剪切應力與速度梯度或剪切速率成正比,可用公式表示為
τ=μ(dvx/dy)= μγ具有黏性的流體在發生形變時將產生阻力。一般情況下,半徑為R的小球以速度v運動時,所受到的流體阻力可用公式f=6πηRv表示(η表示黏性系數)
從本質上講,流體的粘滯性其實就是一種摩擦現象,日常生活中,我們走路,坐定和工作都離不開摩擦,摩擦是普遍存在的。我們特定地將流體的這種摩擦現象稱為粘滯性。物理學上用粘滯系數η來表示流體粘滯性的大小(單位為泊)。例如,20攝氏度時,水的粘滯系數為1.0087厘泊,空氣則要小得多。對于大多數液體,η隨溫度升高而下降,氣體的η則隨溫度升高而上升。1957年12月1日,美國加州理工學院宣布:在液氦Ⅱ里,粘滯系數小得測量不到。它是沒有粘滯系數的理想流體。
運動液體中的摩擦力是液體分子間的動量交換和內聚力作用的結果。液體溫度升高時粘性減小,這是因為液體分子間的內聚力隨溫度的升高而減小,而動量交換對液體的粘滯作用不大。氣體的粘性主要是由于分子間的動量交換引起的,溫度升高則動量交換加劇,因此氣體的粘性隨溫度的升高而增大。

(3)層流、湍流與雷諾數對流動狀態的判定
當流體的流速很小時,流體分層流動,互不混合,稱為層流,也稱為穩流或片流,逐漸增加流速,流體的流線開始出現波浪狀的擺動,擺動的頻率及振幅隨流速的增加而增加,此種流況稱為過渡流;當流速增加到很大時,流線已不再清晰可辨,流場中形成許多小旋渦,層流被破壞,相鄰層間不但有滑動,還有混合。這時的流體做不規則流動,并且有垂直于流管軸線方向的分速度產生,這種運動稱為湍流,又稱為紊流、亂流。
日常生活中,流速較慢,或黏性系數較大的流體的流動一般為層流,例如油,人體內靜脈血液的流動,等等。而流速較大、黏性系數較小的流體流動通常是作湍流,如江河急流,空氣流動、煙囪排煙等都是湍流。
由于湍流的流動具有雜亂性、無規律性和不確定性,因此如何準確地描述湍流至今仍是物理學界的一大難題。
我們通常用雷諾數來判定流體是在做層流還是湍流。
雷諾數是一種可以用來表示流體流動情況的無量綱數,用Re表示。Re=ρvd/η
其中,v, ρ, η分別表示流體的流速,密度與黏性系數,d為一種特征長度。例如流體流過圓形管道,則d表示管道直徑,對于外流問題,v,d一般到遠前方來流速度和物體主要尺寸(如機翼弦長或圓球直徑),內流問題則取通道內平均流速和通道直徑。雷諾數表示作用于流體微團的慣性力與粘滯力之比,如果兩個幾何相似流場的雷諾數相等,則對應微團的慣性力與粘性力之比相等。
雷諾數較小時,黏滯力對流場的影響大于慣性力,流場中流速的擾動會因黏滯力而衰減,此時流體的流動為層流,且流動穩定。當雷諾數較大時,慣性力的影響大于黏滯力,流體的流動較不穩定,流速的微小變化容易發展、增強、形成紊亂、不規則的紊亂流場,即湍流。
由雷諾數的公式可知,當流體的流速較小,或黏性系數較大時,比如油液、潤滑膜內的流動,其粘性影響遍及全流場,雷諾數較小,反之,當流體的流速很大時,比如一般飛行器的繞流,其雷諾數則要大得多,此時,粘性的影響僅在物面附近的邊界層或尾跡中才是重要的。對于F1賽車而言,流過車身的氣流的雷諾數相當可觀,因此流過F1賽車的氣流一定是湍流。

筆者注:

在很多涉及粘性影響的流體力學實驗中,雷諾數是主要的相似準數。但很多模型實驗的雷諾數遠遠小于實物的雷諾數,因此研究修正方法和發展高雷諾數實驗設備是流體力學研究的重要課題。
一般來說,Re <2300為層流狀態,Re> 4000為湍流狀態,Re= 2300 -4000為過渡狀態。在不同的流動狀態下,流體的運動規律、流速分布等都是不同的。因而管道內流體的平均流速v與最大流速Vmax的比值也是不同的,因此流體流動的特性由雷諾數決定。

典型的雷諾數:
普通航空飛機: 5 000 000
小型無人機: 400 000
海鷗: 100 000
滑翔蝴蝶: 7 000
圓形光滑管道: 2 320
橡膠管道: 1 600-2 100
主動脈中的血流: 1 000
大腦中的血液流 : 100
精子: 0.0001

(4)、氣動阻力
阻力,又稱后曳力,空氣阻力或流體阻力,是物體在流場中相對運動所產生與運動方向相反的力。阻力方向和其所在流場的速度方向相反。一般摩擦力不隨速度的變化而變化,但阻力會隨速度而變化。
對于一個在流體中移動的物體,阻力為周圍流體對物體的施力在移動方向的反方向上分量的總和。而施力和移動方向垂直的分量一般則視為升力。因此阻力和物體移動方向相反。
阻力與摩擦力不同,因為摩擦力有時可以是動力。
車輛在行駛時,所要克服的阻力有機件損耗阻力、輪胎產生的滾動阻力(路阻)及空氣阻力。隨著車速的增加,空氣了阻力也逐漸成為最主要的行車阻力,在時速200km/h以上時,空氣阻力幾乎占有所有行車阻力的85%。
空氣阻力系數,又稱風阻系數,是計算汽車空氣阻力的一個重要參數。它是通過風洞實驗和下滑實驗所確定的一個重要參數,用它可以計算出汽車在行駛時的空氣阻力。風阻系數的大小取決于汽車的外形。風阻系數越大,則空氣阻力越大,現代汽車的風阻系數在0.3-0.5之間,賽車可以達到0.15,目前雨滴的風阻系數最小,為0.05左右。
“雨滴”外形對F1賽車的設計具有借鑒意義。由于雨滴形風阻系數最小,所以F1賽車的底盤也可以制作成類似的形狀以減小阻力。例如,紅牛RB7賽車就使用了水滴形狀的底盤,這使得RB7擁有了同賽季所有賽車中最小的氣動阻力,維特爾在斯帕、蒙扎的勝利與其是分不開的。再搭配上功效強勁的廢驅擴散器,使RB7能夠適應各種賽道,成為名副其實的“火星賽車”。

對于車輛行駛時的空氣阻力,一般有三種形式:
一是氣流撞擊車輛正面所產生的阻力,就像拿一塊木板頂風而行,所受到的阻力幾乎都是氣流撞擊所產生的阻力。
二是摩擦阻力,空氣劃過車身一樣會產生摩擦力,然而以一般車輛行駛的最快速度來說,摩擦阻力小到可以忽略。
三是外形阻力。一般來說,車輛調整行駛時,外形阻力是最主要的空氣阻力來源。外形阻力來自車后方的真空區,真空區越大,阻力就越大。一般來說,三廂式的房車外形阻力會比掀背休旅車小。
風阻系數可通過風洞測得。當車輛在風洞中測試時,借由風速來模擬汽車行駛的車速,使車不至于被風吹得后退。在測得所需力后,扣除摩擦,剩下的就是風阻力。結合公式進行計算
Cd=正面風阻力 ×2/(空氣密度× 車頭正面投影面積×車速的平方)
一輛車的風阻系數是固定的,根據風阻系數即可算出車輛在各種速度下所受的阻力。

(5)、邊界層理論

當流體在大雷諾數條件下運動時,可把流體的粘性和導熱看成集中作用在流體表面的薄層即邊界層內。根據邊界層的這一特點,簡化納維-斯托克斯方程,并加以求解,即可得到阻力和傳熱規律。這一理論是德國物理學家L.普朗特于1904年提出的,它為粘性不可壓縮流體動力學的發展創造了條件。

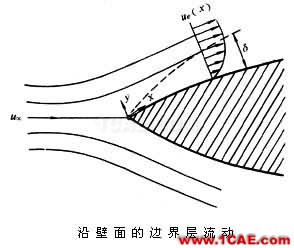
流體在大雷諾數下作繞流流動時,在離固體壁面較遠處,粘性力比慣性力小得多,可以忽略;但在固體壁面附近的薄層中,粘性力的影響則不能忽略,沿壁面法線方向存在相當大的速度梯度,這一薄層叫做邊界層。流體的雷諾數越大,邊界層越薄。從邊界層內的流動過渡到外部流動是漸變的, 所以邊界層的厚度δ通常定義為從物面到約等于99%的外部流動速度處的垂直距離,它隨著離物體前緣的距離增加而增大。根據雷諾數的大小,邊界層內的流動有層流與湍流兩種形態。一般上游為層流邊界層,下游從某處以后轉變為湍流,且邊界層急劇增厚。層流和湍流之間有一過渡區。當所繞流的物體被加熱(或冷卻)或高速氣流掠過物體時,在鄰近物面的薄層區域有很大的溫度梯度,這一薄層稱為熱邊界層。

分析方法

大雷諾數的繞流流動可分為兩個區,即很薄的一層邊界層區和邊界層以外的無粘性流動區。因此,處理粘性流體的方法是:略去粘性和熱傳導,把流場計算出來,然后用這樣的初次近似求得的物體表面上的壓力、速度和溫度分布作為邊界層外邊界條件去解這一物體的邊界層問題。算出邊界層就可算出物面上的阻力和傳熱量。如此的迭代程序使問題求解大為簡化,這就是經典的普朗特邊界層理論的基本方法。

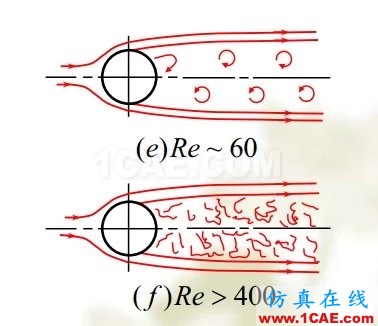
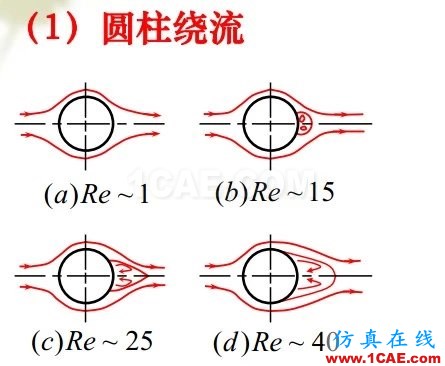
邊界層脫離物面并在物面附近出現回流的現象。當邊界層外流壓力沿流動方向增加得足夠快時,與流動方向相反的壓差作用力和壁面粘性阻力使邊界層內流體的動量減少,從而在物面某處開始產生分離,形成回流區或漩渦,導致很大的能量耗散。繞流過圓柱、圓球等鈍頭物體后的流動,角度大的錐形擴散管內的流動是這種分離的典型例子。分離區沿物面的壓力分布與按無粘性流體計算的結果有很大出入,常由實驗決定。邊界層分離區域大的繞流物體,由于物面壓力發生大的變化,物體前后壓力明顯不平衡,一般存在著比粘性摩擦阻力大得多的壓差阻力(又稱形阻)。當層流邊界層在到達分離點前已轉變為湍流時,由于湍流的強烈混合效應,分離點會后移。這樣,雖然增大了摩擦阻力,但壓差阻力大為降低,從而減少能量損失。

邊界層理論指導著F1賽車的發展,對流體力學的研究作出了重要貢獻。

(6)、伯努利方程

伯努利方程是理想流體定常流動的狀態方程,意為流體在忽略粘性損失的流動中,流線上任意兩點的壓力勢能、動能與位勢能之和保持不變。

理想正流體在有勢體積力作用下作定常運動時,運動方程(即歐拉方程)沿流線積分而得到的表達運動流體機械能守恒的方程。因著名的瑞士科學家D.伯努利于1738年提出而得名。

對于重力場中的不可壓縮均質流體,方程表示為:

P+ρgh+1/2ρv2=c

p、ρ 、v分別表示流體的壓強、密度和速度,h為鉛垂高度,g為重力加速度,c為常量。

上式各項分別表示單位體積流體的壓力能p重力勢能ρgh和動能1/2ρv2,在沿流線運動的過程中,總和保持不變,即總能量守恒。但各流線之間總能量(即上式中的常量值)可能不同。補充:

p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2

p+ρgh+1/2ρv2=常量

均為伯努利方程,其中1/2ρv2 與流速有關,稱為動壓強, p和 ρgh稱為靜壓強。伯努利方程揭示流體在重力場中流動時的能量守恒。

如果研究的是氣體,那么重力的影響就可以忽略不計,公式化簡為P+1/2ρv2=常量(p0)

各項分別稱為靜壓、動壓和總壓。顯然,流動中速度增大,壓強就減小,速度減小,壓強就增大,速度降為零,壓強就達到最大(理論上應等于總壓)。F1翼片產生下壓力,就在于下翼而速度高而壓強小,上翼面速度低而壓強大,因而合力向下。

據此方程,測量流體的總壓、靜壓卻可求得速度,成為皮托管的測速原理。在無旋流動中,也可利用無旋條件積分歐拉方程而得到相同的結果,但涵義不同,此時公式中的常量在全流場不變,表示各流線上流體有相同的總能量,方程適用于全流場任意兩點間。在粘性流動中,粘性摩擦力消耗機械能而產生熱,機械能不守恒,推廣使用伯努利方程時,應該加入機械能損失項。

由伯努利方程可以看出,流速大處壓力低,流速小處壓力高,需要強調的是,伯努利方程的推導假設是固體靜止不動,因此在應用伯努利方程時,需要變換參照系,結果是伯努利方程中的v不是物體的實際運動速度,而是物體與流體相對運動的速度,比如,飛機在逆風起飛時會獲得比順風更好的起飛效果,而F1賽車在制動點的選擇上也受到類似的影響,逆風時可以產生更多的下壓力(特別是前部),制動距離縮短,車手可以更晚地踩下剎車,而順風時氣動效應被削弱,制遠距離延長,車手不得不更早地放開油門制動,這一點在馬來西亞雪邦賽道的9號彎和15號彎最為明顯,進兩個彎之前賽車的行進方向剛好相反,通常一個彎之前的制動距離被縮短,就意味著另一個彎前的制動距離被延長。

(7)、文丘里效應

文丘里效應,又稱文氏效應。這種現象以其發現者,意大利物理學家文丘里命名。這種效應可以制作出文丘里管。

當氣體或液體在文丘理管里面流動,在管道的最窄處,動態壓力(速度)達到最大值,靜態壓力(靜息壓力)達到最小值。氣體(液體)的速度因為涌流橫截面積變化的關系而上升。整個涌流都要在同一時間能經歷縮小的過程,因而壓力也在同一時間減小。進而產生壓力差,這個壓力差用于測量或者給流體提供外在吸引力。

對于理想流體(液體或氣體,其不可壓縮和不具有摩擦),其壓力差通過伯努利方程獲得。

文丘里效應的原理則是當風吹過阻擋物時,在阻擋物的背風面上方端口附近氣壓相對較低,從而產生吸附作用并導致空氣的流動。文丘里管的原理其實很簡單,它就是把氣流由粗變細,以加快氣體流速,使氣體在文氏管出口的后側形成一個“真空”區。當這個真空區靠近工件時會對工件產生一定的吸附作用。

壓縮空氣從文丘里管的入口進入 ,少部分通過截面很小的噴管排出。隨之截面逐漸減小,壓縮空氣的壓強減小,流速變大,這時就在吸附腔的進口內產生一個真空度,致使因周圍空氣被吸入文氏管內,隨著壓縮空氣一起流進擴散腔內減小氣體的流速,之后通過消音裝置減小氣流震蕩。

文丘里效應對于F1賽車的擴散器具有借鑒意義。

(8)、康達效應

康達效應(Coanda Effect)亦稱附壁作用或柯恩達效應。流體(水流或氣流)有離開本來的運動方向,改為隨著凸出的物體表面摩擦時,流體的流速會減慢。只要物體表面的曲率不是很大,依據流體力學中的伯努利原理,流速的減緩會導致流體被吸附在物體的表面上流動。這中作用是以羅馬尼亞發明家亨利-康達命名。

Coanda效應指出,如果平順地流動的流體經過具有彎度的凸表面的時候,有向凸表面吸附的趨向。打開自來水的時候,如果用筷子去觸碰水柱(只要部分水柱即可,這樣現象更明顯),水會隨著筷子向下淌,而不是按重力的方向從水龍頭直接往下流。

康達效應被廣泛地應用到了2012年規則框架下的F1賽車上,康達效應排氣管使得廢氣由底盤吹出重新成為了可能,(具體的問題,我們會在之后的文章中專題分析)

(9)、地面效應

嚴格來講,地面效應的概念只適用于在高速空氣動力學。飛機的翼尖渦流是這一理念被引入的主要原因。當飛機機翼進入高速狀態時,其下表面的高壓氣流往往會越界翻滾到機翼上表面擾亂低壓氣流,從而形成誘導阻力。降低機翼的升阻比,導致機翼效率大降。而當飛機近地飛行時,由于與地面之前的空間更為有限,機翼下部的氣流層便會更加的平穩,從而擾亂翼尖渦流。在沒有翼尖渦流的情況下,機翼的攻角能變得更為接近理論水平,因此便使飛機更有效率。這就是地面效應真正的作用。同時很多只在地效區域飛行的地效飛行器,也是利用這種原理來獲得更優質的升力,來提升機翼的效率。

但是在F1領域中,地面效應被賦予了截然不同的概念。F1工程師通過特別設計的底盤(蓮花78,79)或風扇(布拉漢姆車隊創造的BT46B型風扇底盤賽車),人為地制造真空以獲取強大的吸地效應。

離地間隙(賽車底部和賽道表面之間的距離)對提高底盤和擴散器之間的聯系的效用有大的幫助,賽車的底板是最重要的空氣動力附加裝置。底盤和賽道之間的離地間隙越小,該區域氣流運動的速度也就越大,根據伯努利方程,此區域的靜壓力也就減小,賽車所受的氣動負升力也就越大,使得賽車被強烈地“吸附”在賽道上,產生所謂的“地面效應”。地面效應曾被F1車隊用來提高車速,但為防止追求更高的轉彎速度而引發事故,FIA規定賽車前輪后后緣到后輪前緣部必須平直,限制了地面效應的充分應用。由此FIA規則規定賽車底盤上必須要安裝一志10mm厚的木板,若此木板低于9mm,該車會被取消參賽資格。

獨立的底板是安裝在每輛賽車底部的中間位置(從前到后)的硬木板,通過螺栓與承載式車身下側相連接,通過賽的對木板的磨損程度的檢查可判斷車輛底盤是否過低。

最早運用地面效應于賽車運動中的時間是20世紀70年代,當時考林-查普曼在蓮花賽車底部安裝一個空氣通道,通過前面的部分相對狹窄,但在向車尾延伸的同時不斷擴大。由于賽車的底部離地間隙很小,所以通道和地面形成了一個封閉管道。當賽車飛馳時,空氣從車頭進入,在底盤和地面之間加速,產生非常低的壓強,從而產生向下的壓力。

時下賽車底部的設計多趨于部分或完全覆蓋——從理論上分析,對于完全由光滑底板覆蓋的車底而言,離地高度越低,進入賽車底部前段的氣流速度越快,在車底形成的負壓區就越可觀。現在F1賽車的底盤的形式多采用階梯型,已經不會產生太多的地面效應,擴散器就變得更加重要。

當今也存在F1設計師將車底設計成從前向后升高或設置縱向凹槽的形式,地面與車底部的凹槽構成拉伐爾管,亞聲速氣流在該管收縮段被加速,車身底部與車身上表面的壓力差增加,即增加了下壓力,拉伐爾管道的橫截面形狀、管道截面面積沿注射的變化等都影響車身底部的流態。

為了更好地提高F1賽車的下壓力,空氣動力學工程師運用拉伐爾管效應在賽車底部的兩側裝上整流裙,整流裙剛好接觸路面以密封底部氣流,使得車身降至20mm,仍然取得了很好的氣動效果。

滑動裙(sliding skirts)是安裝在賽車兩側散熱箱側面底部的風翼,它阻止側面氣流通過賽車底部而使賽車底部形成真空,以此將賽車吸附在賽道上并增加賽車在變產中的側身附著力,成功地運用了地面效應。

另一輛應用地面效應創造下壓力的賽車就是戈登-穆雷開發的布拉漢姆BT46B賽車。然而與前者不同的是,由于BT46使用的阿爾法羅米歐引擎寬度大,并沒有足夠的空間賽車采用蓮花79那樣的擴散器設計。穆雷決定,他要通過另外一套工作原理建立起賽車底部的真空效果——在賽車尾部增設一個巨大的風扇裝置。在賽車尾部安裝了一個由引擎自主驅動的風扇裝置。引擎轉速越快,這個裝置吸引賽車底部傳來的空氣就越多,由此建立起上述效果。像查普曼的蓮花賽車一樣,BT46B也安裝了側裙用以維持車下的低壓區,但并未對賽車外形造成改變。然而同年內,圍場中的眾多車隊都譴責這一爭議涉及,稱其違反了“不可移動空氣動力裝置”調理。因此布拉漢姆車隊的所有者伯尼-埃克萊斯頓決定從賽車系列中拿掉BT46B,避免引起其他車隊的爭議。國際汽聯隨后將這款賽車的風扇裝置視作“可移動空氣動力裝置”,對它施行了永久性禁令。

(10)、失速現象

在流體動力學中,失速是指翼型氣動攻角增加到一定程度(達到臨界值)時,翼型所產生的升力突然減小的一種狀態。翼型氣動迎角超過該臨界值之前,翼型的升力是隨迎角增加而遞增的;但是迎角超過該臨界值后,翼型的升力將遞減。

簡單來說,飛機失速意味著機翼上產生的升力突然減少,從而導致飛機的飛行高度快速降低。注意失速并不意味著引擎停止了工作或是飛機失去了前進的速度。

0°迎角繞流 5°迎角繞流

15°迎角繞流 20°迎角繞流

通過以上四幅圖,我們可以看到,當翼片的氣動迎角超過某個值時,附著在翼片上的氣流就會和翼片本身分離,在區域內形成分離渦,這樣一來,下壓力或升力也就要相對減小。

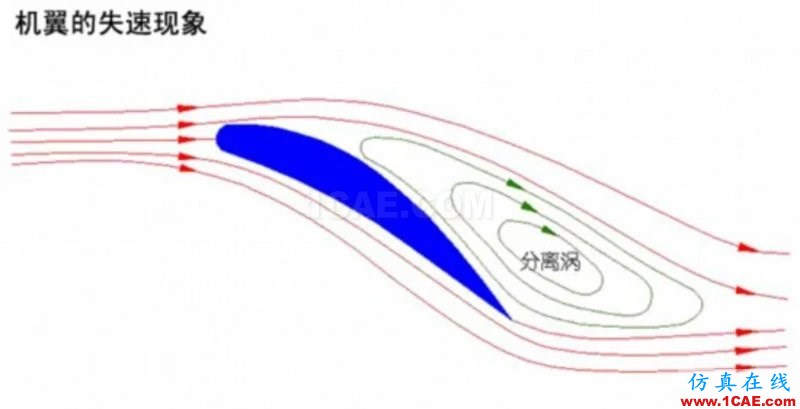
在F1領域,失速現象被廣泛地運用到減阻設計中,但是與航空領域不同的是,F1的翼片不能隨意地更改氣動攻角,因此,在F1領域創造失速現象的理論出發點就確立了:通過某種手段,阻礙翼片上下氣流的會合。即將翼片下方的氣流破壞,而最常見的手段就是吹氣:通過一股突然介入的氣流破壞翼片下方原有的環境,進而影響翼下氣流的運動路徑,創造失速。

邁凱倫在其2010年的MP4-25賽車上使用一種以失速現象為基礎原理的尾翼,這款尾翼在該賽季取得了巨大的成功,并立即被法拉利、紅牛、奔馳、雷諾等隊效仿,成為了2010賽季的“爭冠必備武器”。

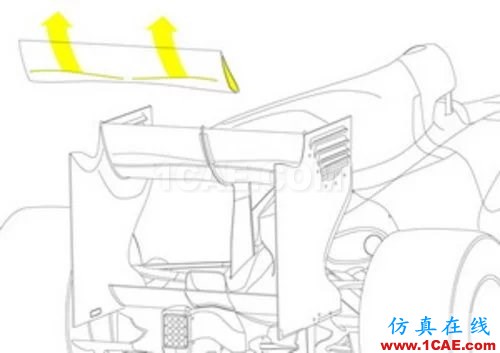
上圖展示了失速尾翼的工作原理,邁凱倫的工程師們將氣流送到了尾翼的下部,這股額外的“不速之客”在尾翼的后方制造了渦流,這樣一來便破壞了尾翼下表面的氣流,使之無法與上表面的氣流匯合。失速現象便由此制造出來。這樣一來尾翼所制造的下壓力就可以忽略不計,賽車在直道上的阻力就被大幅度降低,這種情況下引擎就可以為為賽車提供更大限度的動力輸出,賽車就可以獲得顯著的尾速優勢,賽季初期,邁凱倫的兩輛賽車在尾速方面連續幾站包攬前二,更恐怖的是,MP4-25的極速比排在第二名的車隊快了6-10公里,這也是為何各隊紛紛效仿邁凱倫的原因了。

在此之后,運用失速現象的奔馳,紅牛DDRS又使這項技術在F1領域中進入了更加成熟的新階段。

第二

空氣動力學在F1領域中的實際應用以及F1賽車的氣動特性淺析

一輛F1賽車可以在5秒內加速到200km/h以上,極速更是高達350km/h,但是如果在彎道中輪胎沒有足夠的抓地力,那么引擎即使有足夠強勁的動力,也沒有機會充分發揮。因此過彎穩定性可以極大程度地影響一輛F1賽車的綜合性能。為了提高過彎速度,除了要設置合適的懸架保證輪胎能最大限度地與路面接觸之外,還利用空氣提供額外的氣動負升力,即氣動下壓力。

對于輪胎來說,施加在輪胎上的載荷有三類:車身自重、車手體重和行駛過程中空氣提供的下壓力。其中,氣動下壓力可以在不增加額外質量的前提下,提高輪胎的附著力,有效地提升賽車的過彎性能,甚至直接影響到車手的單圈成績。在引擎研發相對穩定的框架下,對于下壓力的壓榨的開發被放在了新車研發的首要位置。

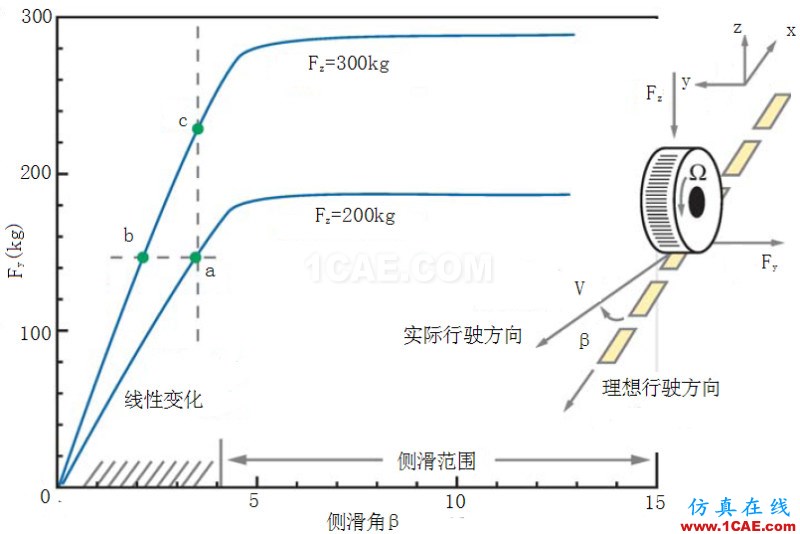
輪胎側滑角與車輪載荷的關系。

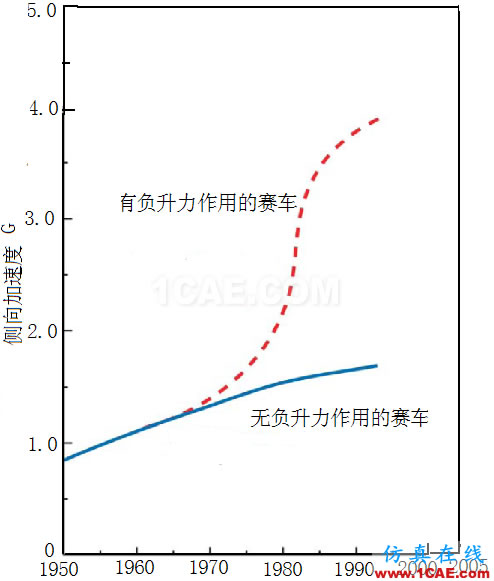
側向加速度與負升力的關系。

下面的文章將利用前面介紹的理論探討F1賽車的氣動問題。

對于目前的F1賽車而言,底盤、發動機和懸架是一輛賽車的必備組成成分,其余的部件則是為了滿足空氣動力學的的需要面安裝的,這此換們稱之為“氣動附加裝置”又可以分為兩類,一類是直接用來產生氣動負升力的裝置,包括前翼、后翼和擴散器,壓力配比方面,前翼產生的下壓力占全部下壓力的30%,尾翼占30%,擴散器占40%。另一類則是用來提升前、后翼以及擴散器的工作效率的輔助性裝置,這此裝置通過提升氣流的傳輸效率,間接地提升賽車的氣動性能,這類裝置包括鼻錐及其下方的導流板,側箱前方的導流板等等。首先,我們就先從前后翼以及擴散器展開對F1賽車氣動特性的討論。

前翼

前翼是安裝在車體最前端的氣動附加裝置,它不僅負責制造賽車前部的下壓力,還影響向后流動的氣流的走向。

前翼由主要結構和眾多的附加結構組成,(這一點是前翼的不斷發展與深化造成的,因此筆者的分類標準并不絕對唯一,僅供參考)。最前端的水平翼片稱為主翼,其后端帶有攻角的傾斜翼片稱為襟翼,理論上來說,只要擁有主翼和襟翼就可以產生下壓力,因此可以將主翼和襟翼概括為前翼的主要結構(但是顯然大家都沒有見過這種前翼,因為即使是2009年使用的那種原始的前翼也都安裝了垂直的端板,但是端板僅僅是一種提高主翼和襟翼工作性能的輔助性裝置,因此以氣動特性上來說,應將其劃分為附加裝置,之后的附加級聯翼片,導流片亦是如此)。

人類在流體力學的研究過程中一直在發展,進步,在可以產生氣動負升力的翼形的研究中更是如此,先后出現了伯努利,牛頓等不同時期的翼形,這些翼形在氣動性能上也不斷提升,今天F1賽車所采用的主襟翼結合的翼形就是人類經過長期探索換來的智慧結晶,這種翼形不僅成熟,而且有效。

F1賽車在高速行駛時,流過前翼所在區域的氣流被前前翼分割為兩部分:一部分從翼片的上表面流過,另一部分則流過翼片的下表面,這兩股氣流依附在翼片上流動,最后在前翼后方的某一區域重新匯聚,兩股的氣流的區別在于,由于襟翼與主翼呈一個很大的傾角,因此襟翼擁有較大的迎風面積,在氣體的流動過程中,翼片上表面的氣流在流動中受到了阻礙,流速有所降低,而翼片下表面的氣流則可以在無阻礙的狀態下順利通過,結合前文提到過的運用在氣體領域的伯努利方程p+1/2ρv2=P0 ,上翼面的氣流流速低,壓強大,下翼面的氣流流速高,壓強小,兩者作差,即產生了我們所需的氣動負升力。襟翼的氣動攻角越大,對翼片上方的氣流的阻礙作用也主越明顯,上、下翼面的流速差就越大,產生的氣動負升力就越大。下圖表示的是前翼和總的氣動負升力與襟翼攻角的關系。

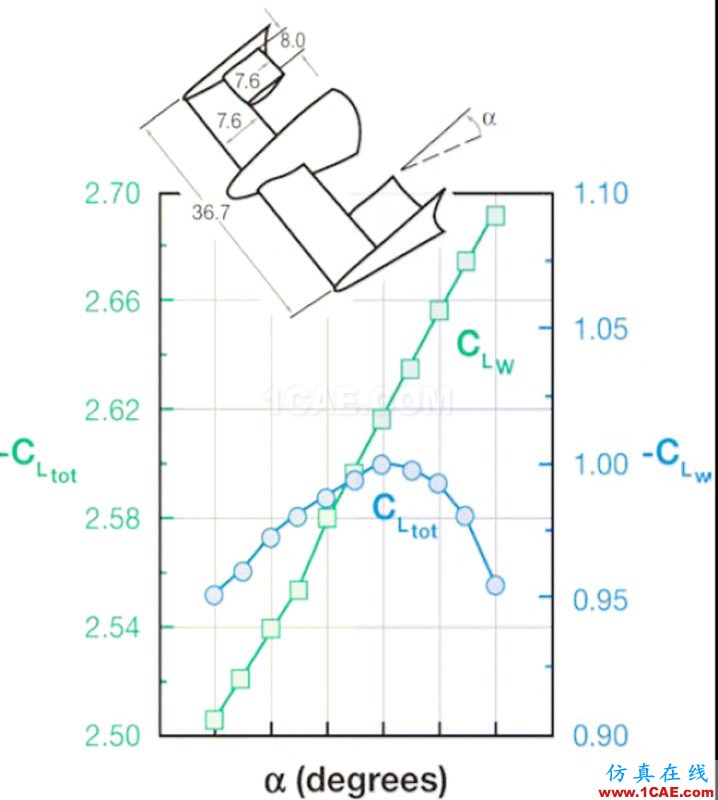
Clw代表前翼的氣動負升力,CLtot代表總的氣動負升力。

但是在這種設置下存在著這樣一個問題:氣動攻角的增加意味著阻力的增加,換言之,增加氣動負升力的同時伴隨著阻力。

下面是前翼產生的氣動阻力隨氣動攻角的數據圖。

CDtot表示總的氣動阻力,CDw表示前翼的氣動阻力

由圖我們可以看出,前翼自身產生的阻力隨氣動攻角的增大而增大,而且二者近似呈線性關系,而賽車整體的氣動阻力則是呈先增大后減小的趨勢。簡單地說明一下,由于前翼位于賽車的最前端,其后就是賽車的前輪,因此這一位置十分特殊,相比之下,氣流直接撞擊在前輪上時產生的阻力要比在前翼上制造下壓力時形成的阻力可觀得多。當襟翼的氣動攻角大到一定程度時,就可以使部分氣流在離開前翼向上擴散的過程中避開前輪,從而減小了氣流撞擊到前輪上的機會,因此,對于整車的氣動阻力而言,當襟翼的攻角超過某一值時,整車的阻力會有所下降,換言之,前翼抵消了部分輪胎上產生的阻力。

對于前翼而言,更大的襟翼攻角和更長的翼弦可以獲得更多的氣動負升力。但是在這兩種設置下下翼面的氣流很容易失去對翼片的依附而與翼面發生分離,我們常稱這一現象為氣流剝離,氣流剝離就會引發前翼失速,降低前翼的氣動負升力水平,因此,常需要在翼面上開槽來解決這一問題,開槽將完整的翼片拆分為若干部分,使得前翼上表面的氣流流入下表面,并保證每一小塊翼片上都時刻有氣流附著,這樣一來就避免了氣流的剝離從而大大地提升了前翼的氣動效率。

F138的前翼開槽。

前翼翼片的工作狀態與航空器有著很大的區別,一個重要的原因是受到了地面效應的影響。一般來說,翼片的離地高度h越小,翼片越靠近地面,地面效應的干預就越強烈,前翼就能制造出更多的氣動負升力,這種現象會一直持續,直到離地高度h小到前翼下表面的氣流難以順利流動。下面這張圖好地表示了這種現象。

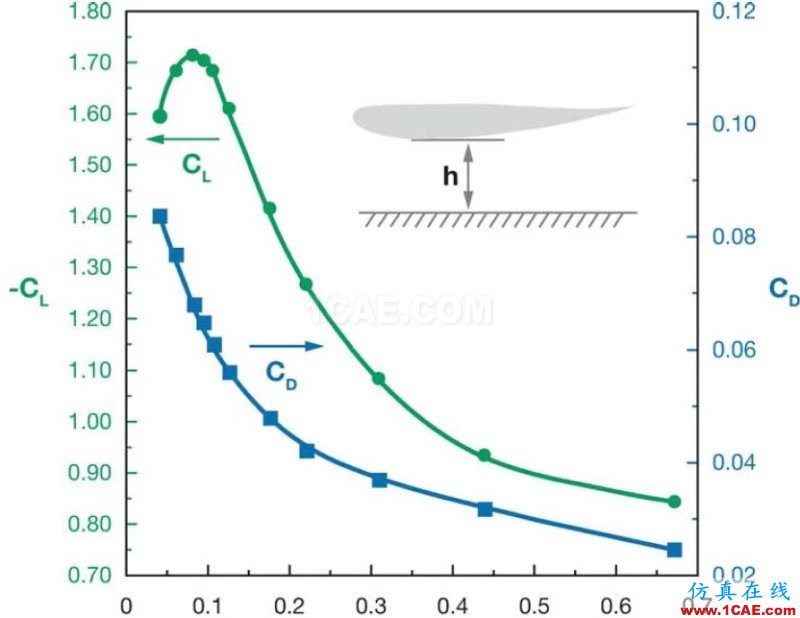
Cl表示負升力系數,Cd表示風阻系數。橫軸表示離地高度。

因此,變形前翼所帶來的氣動優勢不言而喻。

航空領域中翼尖渦流是航空器面臨的一個大麻煩,它不僅形成了巨大的額外阻力,還使得飛行器的升阻比大大下降。對于前翼的翼片來說,上表面的壓強大,下表面的壓強小,這使得部分上翼面的氣流翻到下翼面,同樣破壞了氣動負升力。因此,F1賽車需要安裝端版,將上、下翼面的氣流限制在各自的區域內,提升前翼的氣動效益。

主翼,襟翼和端版構成了一套最原始也是最簡單的前翼。然而隨著空氣動力學的快速發展,F1的工程師們顯然不滿足于這種初始前翼所提供的氣動負升力,于是開始有設計師給前翼安裝附加翼片,以此獲得更多的氣動負升力。在2005-2008年之間,這些附加翼的設計也越發大膽,從R25的小翼面設計到法拉利與鼻錐相連的附加翼,再到邁凱輪橫跨鼻錐的“橋狀附加翼”,F1的設計師對于附加翼的開發似乎永遠都沒有滿足。

雷諾R25的小翼面附加翼。

F2008的大翼面附加翼。

MP4-22的橋狀附加翼。

2009年的技術改革讓F1賽車的前翼呈現出我們今天看到的模式,由于附加翼的安裝位置受到了限制(只能安裝在端版上),因此F1的設計師開始細化附加翼的設計,從原始的單一功能向著多功能的方向演變,現在的附加翼多采用級聯翼片,不僅可以制造額外的氣動負升力,還可以誘導氣流避開前輪。

F1賽車的前翼的工作受到多種因素的影響,首先,作用在翼面上的氣流并不是理想狀態的,風速,風向都時刻變化,且不確定,此外,賽車在彎道中行駛時,作用在翼面上的氣流會發生橫向的偏轉和移動,形成不穩定的流場,這不僅降低了前翼產生的氣動負升力的效率,還影響到了前翼后部的氣流環境,不利于氣流的正常傳輸,針對以上這兩種情況,F1的設計師分別用了如下應對措施:

Ⅰ.增大產生氣動負升力的翼面的有效面積,我們可以注意到,09年改革以前的F1賽車襟翼一直延伸至鼻錐的下方,這就意味著鼻錐下方的翼面上也可以產生氣動負升力。我們以邁凱倫MP4-20的前翼為例,邁凱倫MP4-20的前翼由三片組成,與主翼板吻合,三片翼板都保持著平緩的曲率、中間下沉兩邊高的特征。當低表面的氣流(與前翼處于相同高度的氣流)出現分離、擾動時,前翼受到橫向氣流的影響會被減至最低,因此整個套件非常穩定。賽車的特性是:易于駕駛,敏感程度極低。