基于CAE的試驗的結構動力學有限元模型確認
2013-07-24 by:廣州ANSYS Workbench軟件培訓中心 來源:仿真在線
在航空航天工程中,結構動力學有限元建模是氣動彈性分析的基礎,因此,準確的有限元模型對于氣動彈性的分析至關重要。以提高建模精度為目標的有限元模型修正技術的發展日趨完善,并已逐步在航空、航天領域中得到應用,但是模型修正技術未能全面解決建模精度中存在的問題。建模過程中的不確定因素,比如離散化誤差、材料物理參數的不確定性、邊界條件的近似、缺乏阻尼參數等,將導致有限元模型存在誤差。在設計規范中,有限元模型必須通過模態試驗或者地面共振試驗(GVT)來檢驗。
最近30多年以來,有限元模型修正技術得到快速發展,根據修正的對象的不同可以分為矩陣型修正和元素型修正。元素型修正是以矩陣元素或結構的設計參數為修正對象。其物理意義明確,相對更具有工程應用價值,而本文則主要采用的基于靈敏度分析的設計參數修正方法。
基于靈敏度分析的設計參數型修正方法主要包括待修正設計參數的選擇,靈敏度分析,參數修正以及模型確認等環節。待修正設計參數的選擇是模型修正的起始環節,而候選參數是有限元模型存在不確定性因素的參數。在30多年中,發展了很多種參數選擇或者誤差定位策略與算法,但工程應用中仍然難以準確無遺漏地確定誤差參數。
模型確認通過計算與試驗兩方面的分析,對有限元模型在設計空間的響應預報精度進行評價和確認,并在此基礎上進行模型修正,為進一步的應用提供精確可信的有限元模型以及響應計算方法。因此,有限元模型確認的研究目標有兩個:結合有限的試驗分析,獲得精確可信的確定性的有限元模型;并獲得進行下一步的響應預報所需要的計算參數,其分析的技術流程如圖1所示。
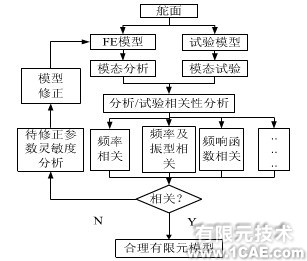
圖1 模型確認流程圖
本文主要是結合了數值分析技術與試驗分析技術,對有限元模型進行修正,然后分析其動力學特性,并將該模型用于后續的顫振分析及結構的動態響應分析中。將有限元法和基于試驗數據的模型確認方法結合成分析結構動力學特性的方法,并驗證該方法的合理性。通過試驗分析數據與修正后的有限元分析數據對比發現,其修正后的有限元精度較高,能夠使該模型適合應用于進一步的分析,為分析復雜結構的動力學特性提供參考。
1 研究模型
本文主要是將有限元法、基于試驗數據的模型確認技術結合起來,準確地對復雜結構進行動力學建模與分析,而本文主要對簡化導彈舵面進行動力學特性的研究,探索并驗證該方法的可行性與適用性。
根據實際導彈的氣動外形,為了加工制造方便,將該導彈舵面簡化為直角梯形,如圖2所示,其上底上底a=0.18m,下底b=0.3m,高h=0.23m,厚度t=0.005m,材料為鋁,彈性模量E1=70GPa,泊松比μ=0.3,而舵軸材料為剛,彈性模量E2=200GPa,泊松比μ=0.3。
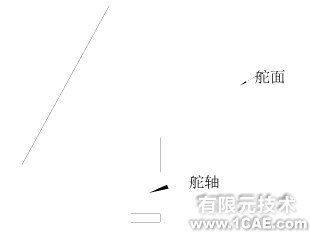
圖2 簡化舵面模型
2 理論方法
2.1 有限元模態分析
有限元模態分析是利用有限元方法確定結構固有頻率和模態的一種計算方法,自由模態分析的整體有限元方程為
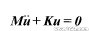
式中M、K分別代表分析模型中的質量矩陣和剛度矩陣,抱歉!圖片加載失敗。(有限元培訓學習,請到1CAE.com學習中心)、u分別代表加速度向量和位移向量。假設結構做簡諧振動,則有
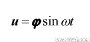
式中φ、ω分別是振型和頻率。將式(1)帶入式(2)可得到特征值方程為
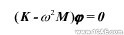
通過求解上述特征值方程,就可以得到結構的固有頻率和相對應的模態,基于有限元方法的模態分析方法就是求解結構的固有頻率和相對應的模態,通過將連續結構離散化,得到結構整體質量矩陣和剛度陣,利用子空間迭代法、Lanczos法、行列式搜索法等求解結構的特征值。該分析結果對實際工程設計有關參數的選擇(比如激振頻率、共振現象的避免與利用等)以及進一步的動力響應分析、氣動彈性動穩定性分析等都很重要,主要是由于結構的固有特性能夠反映結構的動態特性。
2.2 模型確認
2.2.1 相關性理論
為了分析有限元計算的模態或者傳遞函數與試驗測量的模態或者傳遞函數的一致性,可以通過有限元的數據與試驗數據的相關性來進行分析。對于有限元模態與試驗模態的相關性,可以表示為如下公式。
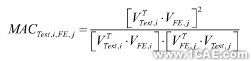
式中VTest,i是第i階試驗模態,VFE,j是第j階有限元模態,MACTest,i,FE,j是第i階試驗模態VTest,i與第j階有限元模態VFE,j的相關性值,MACTest,i,FE,j介于0~1之間,由于有限元模態與試驗模態不可能完全滿足正交性,一般認為有限元模態與試驗模態滿足的相關性值MAC>0.8,就可以認為有限元模態與試驗模態是一致的,如果MAC<0.2,就可以認為有限元模態與試驗模態是正交的。
2.2.2 靈敏度分析
靈敏度是對物理參數的變化率,具體為特征值靈敏度δs/δp和特征矢量靈敏度δψ/δp,其中p代表物理參數。特征值的一階靈敏度一般需要計算質量、剛度陣對設計參變量p的偏導數,在結構動態設計過程中,實際結構簡化為桿、梁、板及殼等單元組成的離散結構模型,此時系統的設計變量p一般取桿單元的橫截面積;梁單元的橫截面積或截面慣性矩;板單元的厚度等。也可以取單元的尺寸和材料常數。
復雜結構的物理參數較多,從結構動力優化設計考慮,必須研究物理參數對其動態特性的靈敏度,這樣才能有效地對結構進行動力修正。但是對于整體結構進行物理參數的靈敏度分析有時較為復雜,于是可以只對部件進行靈敏度分析,修正部件的有限元模型,然后利用動態子結構的方法獲取整體結構的動力學特性。
2.2.3 基于參數的模型修正
基于參數的模型修正對象主要是表征結構特性的物理參數或幾何參數,即設計變量,比如材料彈性模量、密度,桿、梁的橫截面積,板、殼的厚度等。一般,修正的目的是使計算與試驗測量結果(如固有頻率、振型)的誤差最小化。
設設計變量為p,結構的質量和剛度陣M(p),K(p)為其函數,其自由振動的廣義特征值方程為
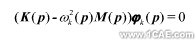
通過求解該特征值方程,可以獲得其固有振動的固有頻率和模態。而第k階特征值ω2k(p)(或固有頻率) fk(p)=ωk(p)/(2/π)和模態φk(p)亦為p的函數。
設實驗測量的固有頻率為,假如僅考慮固有頻率,則固有頻率的計算值fk(p)與實驗結果誤差(目標函數)定義為
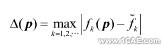
是,基于參數的模型修正可歸為非線性規劃問題
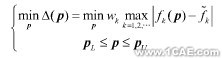
式中pU,pL分別是p的上下限;wk為加權系數。為了方便計算,也可以用平方和代替式(6)中的最大絕對值。一般,式(7)還需要補充強度和剛度條件等約束條件。
對于求解(7)數學規劃問題的方法有直接法和間接法等多種方法。其中的直接法包括經典的最速下降法、擬牛頓法、復合形法,以及現在常用的遺傳算法、模擬退火法等。而當結構出現重頻時,而靈敏度就需要作特殊處理。
3 計算結果與分析
3.1 舵面模態試驗
對于該簡化導彈舵面模型的模態試驗激勵方法主要采用力錘法。數據采集方面主要是利用LMS的SCADAS Ⅲ模態分析設備和PCB加速度傳感器;測試軟件則采用LMS Test.Lab 8B中的Structures Acquisition模塊中的Impact Testing,用于錘擊法試驗模態的采集與分析。
為了獲得舵面模態信息,以及通過試驗后,對有限元模型進行修正,于是在舵面上布置了14個測點,并在固定夾具位置布置一個參考測點,總共15個測點,如圖3所示,分別對4點和14點進行錘擊,所以4點和14點的傳感器布置在Z軸正向,測量Z向的振動。對于顫振分析,一般只需要舵面的一階彎曲頻率和一階扭轉頻率。于是本文中取試驗測得的舵面的前2階固有頻率,如表1所示;前2階模態圖如圖4所示,其MAC圖如圖5所示。

圖3 舵面模態試驗
表1 舵面前2階固有頻率
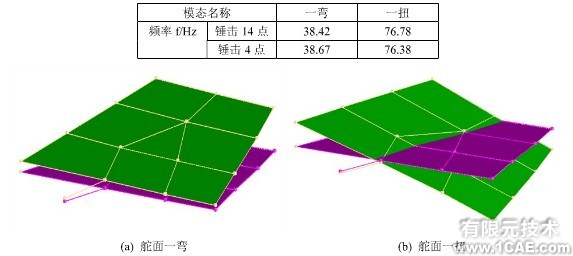
圖4 舵面前2階模態圖

圖5 試驗的MAC圖
通過對不同激勵點激勵所得結果進行對比發現,其固有頻率相差很小,但是通過觀察LMS軟件分析所獲得的模態圖和頻響函數發現,對于錘擊14點所得到的結果更接近實際情況,于是選擇改組數據作為后續的計算。
3.2 舵面模態試驗結果與有限元分析對比
通過對該舵面進行有限元建模,然后進行模態分析,一彎和一扭模態圖如圖6所示,將所得的分析結果與試驗結果進行對比,對比結果如表2所示。如圖7所示,是計算有限元與試驗的MAC值,前2階的MAC值都大于0.9,說明有限元建模分析與試驗分析的相關性較好,但是由于頻率誤差較大,需要對有限元模型進行修正。
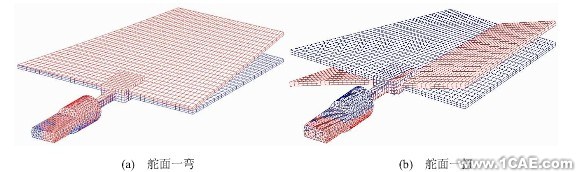
圖6 舵面前2階模態圖
表2 舵面前2階頻率對比和MAC值
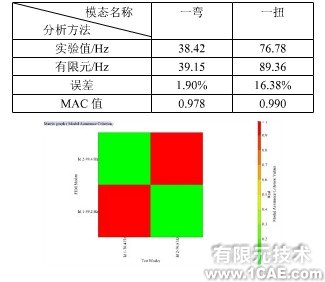
圖7 有限元分析與試驗分析的MAC值
通過試驗分析結果與有限元分析結果對比發現,在第1階誤差相對較小,但是第2階頻率相差較大,這對于顫振分析有很大的影響,于是需要對有限元模型進行修正,然后再利用修正后的模型才能進行下一步分析。
3.3 舵面模型確認
3.3.1 靈敏度計算
由于有限元模型在舵面、舵軸等幾何尺寸都與實際試驗件一樣,于是不需要修改這些幾何尺寸,因而不對這些尺寸進行靈敏度分析。由于該舵面結構相對較簡單,設計變量相對較少,而且受到試驗條件的限制,無法測量試驗件的彈性模量,試驗件中的螺栓連接在有限元模型中是利用的彈簧單元模擬的。因此本文中主要選擇這兩個參數對其進行靈敏度分析,即這些參數變化對固有頻率的影響。其分析的模態頻率對舵軸彈性模量和相關性MAC值對設計變量的靈敏度值如圖8所示。
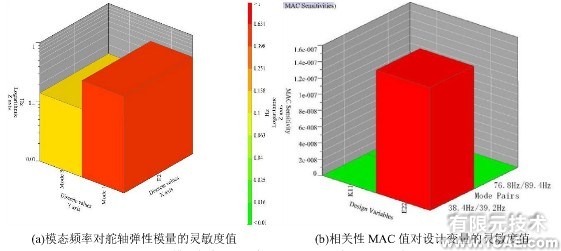
圖8 模態頻率和相關性MAC對設計變量的靈敏度值
通過靈敏度計算可以發現,在一定范圍內,模擬彈簧的剛度值變化主要影響舵面的彎曲頻率,而舵軸的彈性模量則影響彎曲頻率和扭轉頻率。于是需要對這兩個參數進行修正,使得有限元模型所計算的頻率與試驗測量的固有頻率的誤差達到最小值。
3.3.2 舵面模型修正及相關性計算
通過實測試驗件的質量與有限元建模所得到的模型質量對比發現,具有一定的偏差,于是首先需要對有限元模型的密度進行修正,使得每個有限元模型部件的質量特性與試驗件的一樣。并且通過靈敏度分析后,對于本文模型主要是對模擬彈簧單元的剛度值和材料的彈性模量進行參數修正,其參數修正主要利用了MSC.Nastran的優化功能,求解序列為SOL200。主要以模擬彈簧單元的剛度,舵面、舵軸的彈性模量(材料參數) 為設計變量,以頻率誤差最小為目標函數, 以彎曲頻率38.0Hz≤f1≤39.0Hz,扭轉頻率76.0Hz≤f2≤77.0Hz為約束條件進行優化。其修正結果與試驗結果的對比如表3所示,而對修正模型的有限元分析與試驗分析進行相關性分析,其分析的MAC值如表3所示,MAC圖如圖9所示。
表3 修正后舵面前2階頻率對比和MAC值
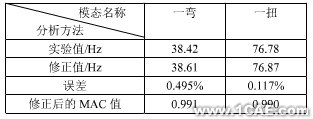
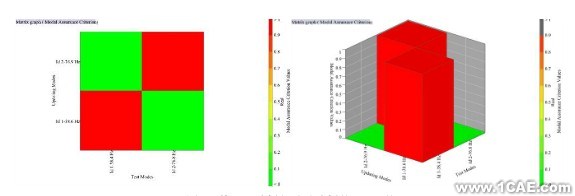
圖9 修正后分析與試驗分析的MAC值
通過表3所示,其修正后的頻率能夠達到很高的精度,并且其修正后的MAC值也都大于0.99,說明修正后的模型與試驗模型的相關性較好,于是該模型可以用于進一步分析。
4 結論
(1)本文主要介紹了基于試驗的結構動力學有限元模型確認方法。對于有限元模型修正涉及的因素比較多,而目前基本沒有一種普適算法進行修正。對于不同情況,綜合應用各種理論方法、參考多組實測數據,結合工程人員的實際工程經驗,才能夠獲得相對客觀、準確的修正模型。
(2)而本文主要利用了試驗數據,對有限元模型與試驗模型的相關性進行分析,然后對有限元模型進行靈敏度分析,獲得需要修正的參數,然后對有限元模型進行修正,通過算例表明該方法能夠得到精確度較高的合理模型,能夠用于顫振分析以及結構的動態響應分析中。
相關標簽搜索:基于CAE的試驗的結構動力學有限元模型確認 CAE分析 廣州ANSYS培訓 Ansys有限元培訓 Ansys workbench培訓 ansys視頻教程 ansys workbench教程 ansys APDL經典教程 ansys資料下載 ansys技術咨詢 ansys基礎知識 ansys代做 Fluent、CFX流體分析






